Géométrie - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Géométrie - Cours Terminale S
Géométrie - Cours Terminale S
Conjugué d'un nombre complexe
Défnition
Tout nombre complexe z admet un conjugué noté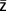 
(que l'on peut lire z barre) qui possède la même partie réelle mais une partie imaginaire opposée:
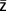= a - ib
Distinguer les réels et les imaginaires purs
Si z est un réel pur alors z = a et puisque que sa partie imaginaire est nulle elle l'est aussi pour son congué donc 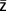= a: un reél pur est égal à son conjugué.
- dL
Si z est un imaginaire pur alors z = ib, son conjuguée possède la même partie réelle (nulle) et une partie imaginaire opposée (-ib) donc 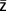= -ib: Un imaginaire est égal à l'opposée de son conjugué.
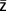
Ces critères peuvent être utilisés pour démontrer qu'un nombre est soit un réel pur soit un imaginaire pur.
Addition d'un nombre complexe et de son conjugué
Soit z un nombre conjugué (z = a + ib) et 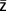son conjugué ( 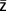= a - ib)
z + 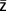= a + ib + a - ib
= a + a +ib - ib
= 2a
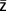= 2Re(z)
La somme d'un nombre complexe et de son conjugué correspond au double de sa partie réelle.
Produit d'un nombre complexe par son conjugué
Soit z un nombre conjugué (z = a + ib) et 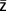son conjugué ( 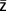= a - ib)
z . 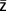= (a + ib)(a - ib)
= a2 - (ib)2 (d'après l'identité remarquable
= a2 - (-b2)
= a2 + b2
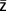= a2 + b2
Le produit d'un nombre complexe par son conjuguée correspond à somme du carré de sa partie réelle et du carré de sa partie imaginaire.
Autres propiétés algébriques des conjugués
Si k est un réel, n un entier, z et z' deux nombres complexes alors :
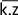= k.
= + '
= . '
= 
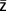
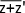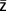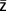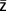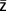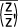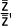
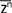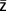= ()n
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
