Les fonctions - Classe de seconde
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Les fonctions - cours de seconde
Etude qualitative de fonctions
Fonctions croissantes et décroissantes
Définitions
Une fonction est dite croissante sur un intervalle I de son ensemble de définition si pour toutes les valeurs x1 et x2 de cet intervalle, telles que x1 ![]() x2, alors f(x1)
x2, alors f(x1)![]() f(x2) (ou encore f(x2)
f(x2) (ou encore f(x2) ![]() f(x1) )
f(x1) )
Une fonction est dite décroissante sur un intervalle I de son ensemble de définition si pour toutes les valeurs x1 et x2 de cet intervalle, telles que x1 ![]() x2, alors f(x1)
x2, alors f(x1) ![]() f(x2) (ou encore f(x2)
f(x2) (ou encore f(x2) ![]() f(x1) )
f(x1) )
Remarque: si une fonction est qualifiée de croissante sans précision d'intervalle cela signifie qu'elle est croissante sur la totalité de son ensemble de définition, de même si une fonction est qualifiée de décroissante sans mention d'intervalle cela sous-entend qu'elle est décroissante sur tout son ensemble de définition.
Exemple:
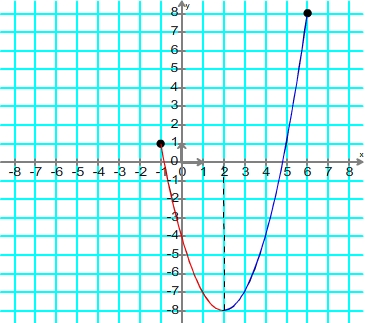
f est décroissante sur l'intervalle [-1 ; 2]
f est croissante sur l'intervalle [2 ; 6]
Compraraison de differentes valeurs
En pratique on exploite plutôt les variations d'une fonction (le fait qu'elle soit croissante ou décroissante) pour comparer ses images.
Si une fonction f est croissante sur un intervalle alors plus la variable est élevée et plus l'image a aussi une valeur élevée. Si par exemple on sait qu'une fontion f est croissante sur un intervalle [0 ; 20] alors on peut déduire que:
f(0) ![]() f(1)
f(1)
f(1) ![]() f(2)
f(2)
f(2) ![]() f(10)
f(10)
f(10)![]() f(20)
f(20)
f(0) ![]() f(20) etc
f(20) etc
Si au contraire une fonction est décroissante sur un intervalle alors plus la variable est élevée et plus le nombre image est petit. Si par exemple on sait qu'une fontion f est décroissante sur un intervalle [-5 ; 15 ] alors on peut déduire que:
f(-5) ![]() f(-4)
f(-4)
f(-4) ![]() f(-3)
f(-3)
f(-3) ![]() f(5)
f(5)
f(5) ![]() f(15)
f(15)
f(-5) ![]() f(-15) etc
f(-15) etc
Minimum et maximum
Sur un intervalle de l'emsemble de définition d'une fonction le maximum correspond au nombre image dont la valeur est la plus élevée.
Sur un intervalle de l'emsemble de définition d'une fonction le minimum correspond au nombre image dont la valeur est la plus petite.
Si une fonction est croissante sur un intervalle alors l'image de la borne inférieure de cet intervalle correspond à un minimum et celle de la borne supérieure est un maximum. Inversement si une fonction est décroissante sur un intervalle alors l'image de la borne inférieure correspond à un maximum tandis que celle de la borne supérieure est un minimum.
Si par exemple on considère de nouveau la fonction f dont la courbe est représentée dans le paragraphe "définition" alors:
Sur l'intervalle [-1 ; 2] f a pour minimum -8 et comme maximum 1
Sur l'intervalle [2 ; 6] f a pour minimum -8 et comme maximum 8
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
