Les fonctions - Classe de seconde

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Les fonctions - cours de seconde

Fonctions de réference

Fonctions linéaires

Définition

Une fonction linéaire est une fonction défine par une formule de forme f(x) = ax
où "a" est une constante réelle positive ou négative appélée coefficient directeur

Par une fonction linéaire, l'image d'un nombre est proportionnelle à ce nombre et le coefficient directeur "a" fait office de corfficient de proportionnalité.

Ensemble de définition

Une fonction linéaire peut toujours être définie sur la totalité de l'ensemble des réels

Courbe représentative

Il s'agit toujours d'une droite passant par l'origine, pour la tracer il suffit donc de connaître un point supplémentaire que l'on peut déterminer à partir de la formule f(x) = ax. Celle-ci permet d'en déduire que l'on peut par exemple utiliser les points (1;a), (2; 2a), (3;3a) etc

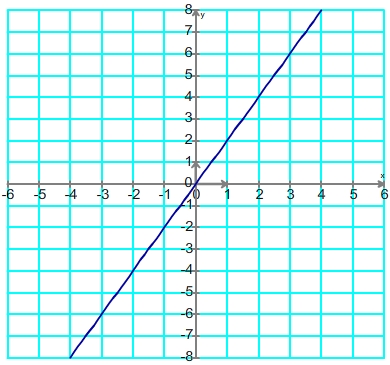
Déterminer la formule d'une fonction linéaire à partir d'un graphique

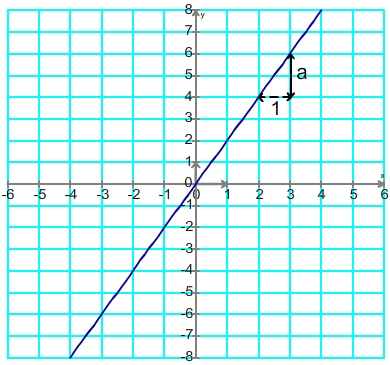
La formule d'une fonction linéaire est caractérisée par son coefficient directeur "a", pour déterminer sa valeur:
- on peut utiliser un point quelconque de la droite de coordonnées ( x₁ ; y₁ ), puisque "a"  on obtient alors en divisant l'ordonnée par l'abscisse
a =   y₁    
        x₁    
- on peut aussi déterminer la variation d'ordonnée de la courbre correspondant à une variation d'une unité de l'abcsisse

Trouver l'antécédent d'un nombre

Par une fonction linéaire chaque nombre de l'ensemble des réels possède un seul et unique antécédent qui peut être déterminer à partir de la formule. Si par une fonction affine f un nombre y₂ a pour antécédent le nombre x₂ alors:
y₂ = ax₂
x₂ =  y₂  
         a    

Variations

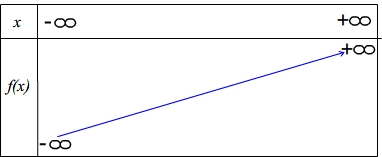
si a>0 (coefficient directeur positif) alors f est croissante sur la totalité de son ensemble de définition

                          Aspect de la courbe                                                                    Tableau de variation

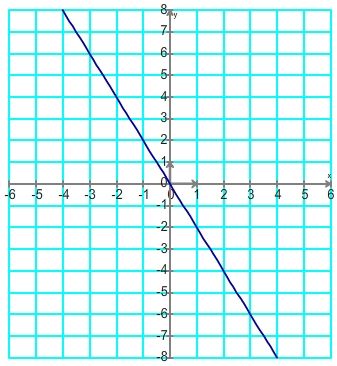
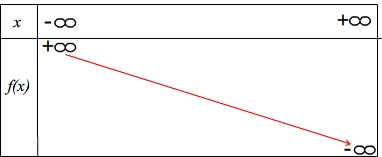
si a<0 (coefficient directeur négatif) alors f est décroissante sur la totalité de son ensmble de définition

Aspect de la courbe      Tableau de variation

Signe

Si le coefficient directeur est positif alors la fonction est négative sur l'intervalle [  ; 0] puis positive sur [ 0 ;  ]

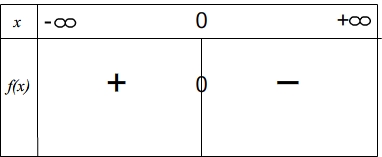
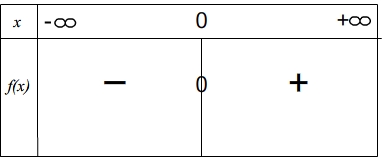
Si le coefficient directeur est négatif alors c'est l'inverse, elle est positive sur l'intervalle [ ; 0] puis négative sur [ 0 ;  ]