Les fonctions - Classe de seconde
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Les fonctions - cours de seconde
Etude qualitative de fonctions
Résoudre graphiquement une inéquation
Une inéquation peut se résoudre de manière algébrique (si sa complexité le permet) mais il est existe aussi une méthode graphique applicable lorsque l'un des termes correspond à une fonction dont on dispose de la courbe.
Résoudre une équation de la forme f(x)
a
Dans cas le terme de gauche de l'inégalité est assimilable à un fonction de variable x tandis que le terme de droite (a) est un nombre réel constant. La méthode de résolution d'une telle inéquation est la suivante.
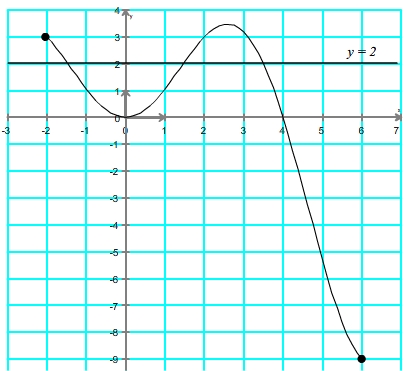
- Etape 1: sur le graphique comportant la courbe représentant la fonction, tracer la droite d'équation y = a (droite horizontale d'abscisse a).
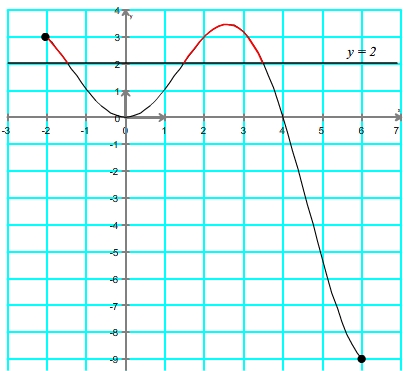
- Etape 2: repérer les zones de la courbe situées au-dessus de la droite tracée.
- Etape 3: déterminer, sur l'axe des abscisses, les intervalles correspondant aux portions de courbe repérées dans l'étape 2.
- Etape 4: la solution de l'inéquation correspond à l'intervalle ou à la réunion d'intervalles obtenu à l'étape 3.
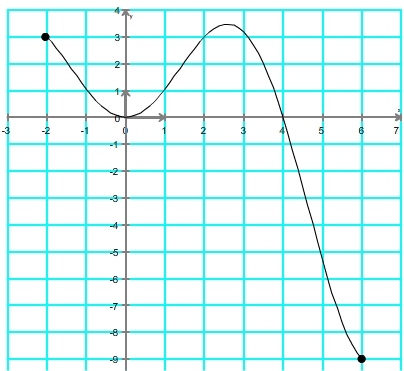
Exemple de la résolution de l'équation f(x) 2 pour la fonction définie par la courbe suivante:
Tracer de la droite d'équation y = 2
Etape 2
Etape 3
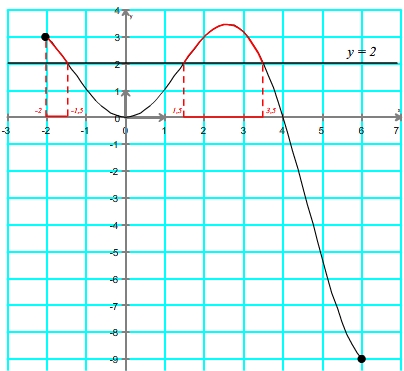
Etape 4
L'ensemble des solutions à l'inéquation f(x)
2 est donc : [-2 ; -1,5] U [1,5 ; 3,5]
Résoudre une inéquation de la forme f(x) 
a
La méthode pour résoudre une telle inéquation est à quelques détails près presque la même que la précédente. Lors de l'étape 2 il suffit de repérer les zones de la courbe qui sont situées sous la droite au lieu de choisir celles qui sont au-dessus.
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
