Les fonctions - Classe de seconde
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Les fonctions - cours de seconde
Chapitre 1: Les fonctions
Fonction définie par une courbe
Il est possible de représenter par une courbe une fonction définie par une formule ou un tableau de valeurs mais une courbe est également un outil qui permet de définir une fonction. Elle doit nécessairement respecter l'une des caractérisques des fonctions qui est de n'associer à un nombre de l'ensemble de définition qu'un seul point image, ce qui implique de faire correspondre à chaque abscisse un seul point de la courbe. Choisir de définir une fonction par une courbe implique certaines restrictions et quelques inconvénients (l'ensemble de définition ne peut être prolongé à l'infini, la lecture des abscisses et des ordonnées peut comporter une certaine part d'imprécision).
Exemple n°1Ensemble de définition Il correspond à l'intervalle des abscisses sur lequel la courbe est représentée, il est nécessairement borné (puisqu'il ne peut se prolonger vers  ou  ) et ses bornes sont l'abscisse la plus petite et celle la plus élevée. Elles peuvent être inclues ou exclues de l'intervalle de définition (en général un point signifie une inclusion et un arc de cercle orienté vers l'extérieur de la courbe signifie une exclusion)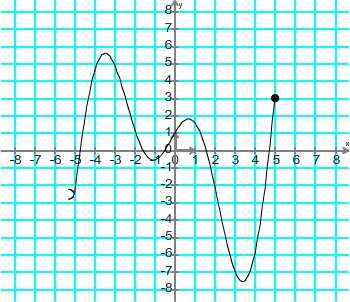 Cette courbe définit une fonction dont l'ensemble définition est ]-5; 5] Exemple n°2
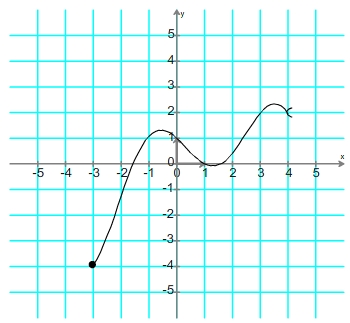 Cette courbe définit une fonction dont l'ensemble définition est [-3; 4[ Trouver l'image d'un point Pour trouver l'image d'un nombre de l'ensemble de définition on procède suivant la méthode suivante: - on repère ce nombre sur l'axe des abscisses (horizontal) - on repère le point de la courbe correspondant à cette abscisse - on détermine l'ordonnée de ce point, elle correspond à l'image du point Exemple: image du nombre 2 par la fonction définie par la courbe de l'exemple n°1 Repérage de l'abscisse correspondant au nombre 2
Trouver le ou les antécédents d'un nombre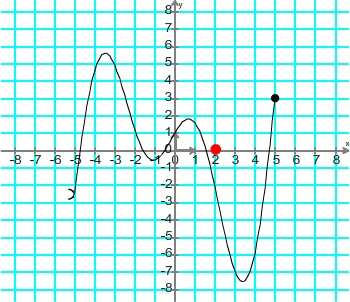 Repérage du point de la courbe d'abscisse correspondant au nombre 2 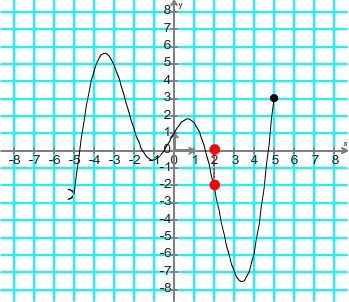 Détermination de l'ordonnée du point d'abscisse 2 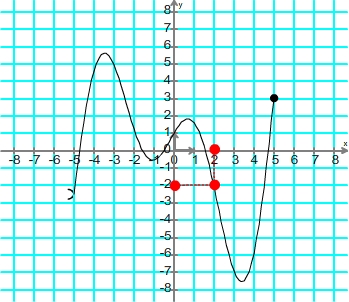 Résultat: l'image du nombre 2 par cette fonction est -2 Pour trouver les antécédents d'un nombre grâce à une courbe on peut suivre la méthode suivante: - Tracer la ligne horizontale dont les points ont ce nombre comme ordonnée - Repérer les point d'intersection entre cette droite et la courbe - Déterminer l'abscisse de ces points d'intersection, elles correspondent aux antécédents recherchés Exemple: antécédents du nombre 1 par la fonction définie par la courbe de l'exemple n°1 Tracé de la droite horizontale d'ordonnée 1
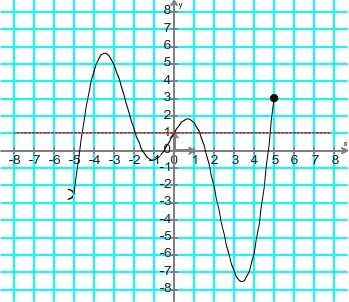 Répérage des points d'intersection 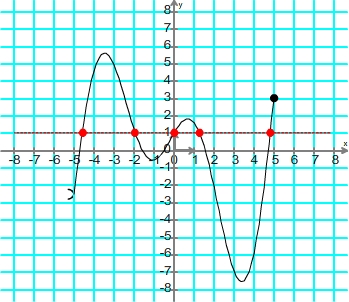 Détermination de l'abscisse des points d'intersection 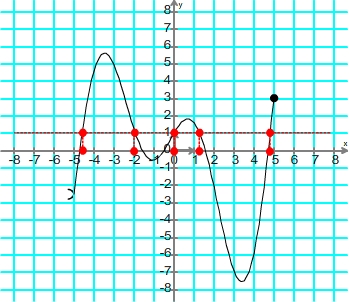 Résultat: le nombre 1 possède 5 antécédents: -4,6 ; -2 ; 0 ; 1,2 et 4,8 |
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
