Les fonctions - Classe de seconde
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Les fonctions - cours de seconde
Fonctions de réference
Fonctions affines
Définition
Une fonction est dite affine si est caractérisée par une formule de type f(x) = ax + b
où:
- "a" est une constante réelle positive ou négative appelée coefficient directeur.
- "b" est une constante réelle positive ou négative appelée ordonnée à l'origine. "b" doit être non nul sinon la formule devient f(x) = ax ce qui caractérise les fonctions linéaires.
Ensemble de définition
Toutes les fonctions affines sont définies sur la totalité de l'ensemble des nombres réels.
Courbe représentative
Il s'agit d'une droite ne passant pas par l'origine (sinon c'est une fonction linéaire) montante ou descendante. Pour la tracer il est nécessaire de connaître deux points qui lui appartiennent. Le premier point que l'on choisit en général (car il ne nécessite pas de calcul) est le point d'abscisse nul, d'après la formule générale d'une fonction affine f(0) = a.0 + b soit f(0) = b donc ses coordonnées sont (0;b). Le deuxième point est souvent l'un de ceux dont l'abscisse est un entier, on choisit donc parmi les points (1 ; a+b), (2 ; 2a +b), (3 ; 3a +b) etc.
Déterminer la formule d'une fonction affine à partir de la droite qui la représente
Une fonction affine est toujours associée à une formule de type f(x) = ax + b, pour déterminer cette formule il faut donc trouver la valeur de "a" et celle "b".
La valeur la plus simple à trouver est celle de "b" car, comme son nom l'indique, elle correspond à l'ordonnée à l'origine, il suffit donc de repérer sur le graphique le point d'intersection entre la droite et l'axe des ordonnées: l'ordonnée de ce point correspond à "b".
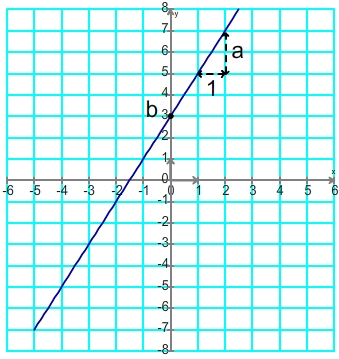 Le coefficient directeur "a" peut être obtenu en déterminant la variation d'ordonnée correspondant à une augmentation d'une unité des abscisses, cette valeur est celle de "a" (méthode déjà utilisée pour les fonctions linéaires).
Le coefficient directeur "a" peut être obtenu en déterminant la variation d'ordonnée correspondant à une augmentation d'une unité des abscisses, cette valeur est celle de "a" (méthode déjà utilisée pour les fonctions linéaires).
Il est également possible de trouver "a" à partir des coordonnées de deux points M1(x1;y1) et M2(x2;y2) de la droite :
a = (y2 – y1)/(x2 – x1)
Autres méthodes pour trouver "a" et "b"
- Lorsque b à été trouvé on peur déterminer la valeur de "a" à partir des coordonnées d'un point M1(x1;y1) de la droite en résolvant l'équation y1 = ax1 + b, on en tire alors a = (y1 – b)/a.
- De même lorsque "a" à été trouvé on peur déterminer la valeur de "b" à partir des coordonnées d'un point M1(x1;y1) de la droite en résolvant l'équation y1 = ax1 + b, on en tire alors b = y1- ax1.
- On peut également choisir de trouver "a"et "b" à partir des coordonnées de deux points de la droite, en résolvant un système de deux équations à deux inconnues:
* y1 = ax1 + b
* y2 = ax2 + b
Antécédent
Par une fonction affine chaque nombre de l'ensemble des réels possède un seul et unique antécédent qui peut être trouvé à partir de la formule dela fonction. Si l'on recherche l'ancédent x1 d'un nombre y1 alors:
y1 = ax1 + b
y1 - b = ax1
ax1 = y1 - b
x1 = y1 - b
a
Variations
Si le coefficient directeur est positif (a>0) alors la fonction affine est croissante sur la totalité de l'ensemble des nombres réels
Aspect de la courbe Tableau de variation
Si le coefficient directeur est négatif (a<0) alors la fonction affine est décroissante sur la totalité de l'ensemble des nombres réels
Aspect de la courbe Tableau de variation
Signe
La fonction affine s'annule pour x0 tel que:
ax0 + b = 0
ax0 = -b
x0 = - b
a
Si le coefficient directeur est positif alors la fonction est négative sur l'intervalle ] ; x0] puis positive sur [ x0 ;
; x0] puis positive sur [ x0 ;  [
[
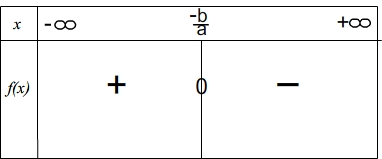
Si le coefficient directeur est négatif alors c'est l'inverse, elle est positive sur l'intervalle ] ; x0] puis négative sur [ x0 ; [
; x0] puis négative sur [ x0 ; [


où:
- "a" est une constante réelle positive ou négative appelée coefficient directeur.
- "b" est une constante réelle positive ou négative appelée ordonnée à l'origine. "b" doit être non nul sinon la formule devient f(x) = ax ce qui caractérise les fonctions linéaires.
Ensemble de définition
Toutes les fonctions affines sont définies sur la totalité de l'ensemble des nombres réels.
Courbe représentative
Il s'agit d'une droite ne passant pas par l'origine (sinon c'est une fonction linéaire) montante ou descendante. Pour la tracer il est nécessaire de connaître deux points qui lui appartiennent. Le premier point que l'on choisit en général (car il ne nécessite pas de calcul) est le point d'abscisse nul, d'après la formule générale d'une fonction affine f(0) = a.0 + b soit f(0) = b donc ses coordonnées sont (0;b). Le deuxième point est souvent l'un de ceux dont l'abscisse est un entier, on choisit donc parmi les points (1 ; a+b), (2 ; 2a +b), (3 ; 3a +b) etc.
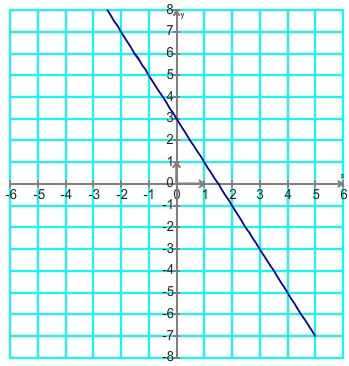
Aspect général de la représentation d'une fonction affine
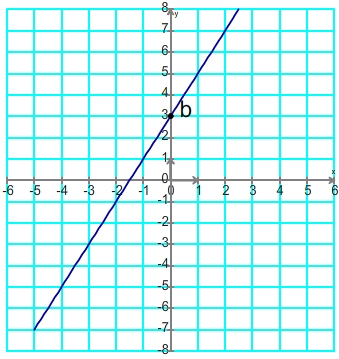

Déterminer la formule d'une fonction affine à partir de la droite qui la représente
Une fonction affine est toujours associée à une formule de type f(x) = ax + b, pour déterminer cette formule il faut donc trouver la valeur de "a" et celle "b".
La valeur la plus simple à trouver est celle de "b" car, comme son nom l'indique, elle correspond à l'ordonnée à l'origine, il suffit donc de repérer sur le graphique le point d'intersection entre la droite et l'axe des ordonnées: l'ordonnée de ce point correspond à "b".

Il est également possible de trouver "a" à partir des coordonnées de deux points M1(x1;y1) et M2(x2;y2) de la droite :
a = (y2 – y1)/(x2 – x1)
Autres méthodes pour trouver "a" et "b"
- Lorsque b à été trouvé on peur déterminer la valeur de "a" à partir des coordonnées d'un point M1(x1;y1) de la droite en résolvant l'équation y1 = ax1 + b, on en tire alors a = (y1 – b)/a.
- De même lorsque "a" à été trouvé on peur déterminer la valeur de "b" à partir des coordonnées d'un point M1(x1;y1) de la droite en résolvant l'équation y1 = ax1 + b, on en tire alors b = y1- ax1.
- On peut également choisir de trouver "a"et "b" à partir des coordonnées de deux points de la droite, en résolvant un système de deux équations à deux inconnues:
* y1 = ax1 + b
* y2 = ax2 + b
Antécédent
Par une fonction affine chaque nombre de l'ensemble des réels possède un seul et unique antécédent qui peut être trouvé à partir de la formule dela fonction. Si l'on recherche l'ancédent x1 d'un nombre y1 alors:
y1 = ax1 + b
y1 - b = ax1
ax1 = y1 - b
x1 = y1 - b
a
Variations
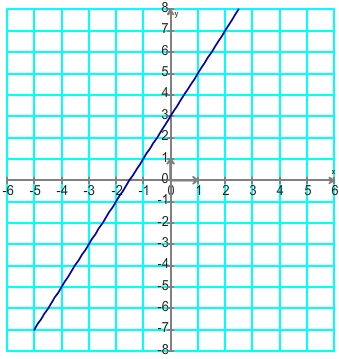
Si le coefficient directeur est positif (a>0) alors la fonction affine est croissante sur la totalité de l'ensemble des nombres réels
Aspect de la courbe Tableau de variation
 |
 |
Si le coefficient directeur est négatif (a<0) alors la fonction affine est décroissante sur la totalité de l'ensemble des nombres réels
Aspect de la courbe Tableau de variation
 |
 |
Signe
La fonction affine s'annule pour x0 tel que:
ax0 + b = 0
ax0 = -b
x0 = - b
a
Si le coefficient directeur est positif alors la fonction est négative sur l'intervalle ]

Si le coefficient directeur est négatif alors c'est l'inverse, elle est positive sur l'intervalle ]

Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
