Les fonctions - Classe de seconde

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Les fonctions - cours de seconde

Etudes de fonctions

Fonctions homographiques

Définition

Une fonction homographique correspond au rapport de deux fonctions affines, sa formule est donc toujours du type:

f(x) =	ax + b
	cx +d

où a, b, c et d sont des constantes réelles positives ou négatives
Avec quelques restrictions:
- c ne doit pas être nulle sinon la formule est celle d'une fonction affine (f(x) = (a/d)x +(b/d))

- c ne doit pas être nulle sinon la formule est celle d'une fonction affine (f(x) =	a x +  b
	d        d

- La fonction affine ax + b ne doit pas être proportionnelle à la seconde sinon le rapport des deux est constant.

Forme réduite d'une fonction homographique

On peut montrer que toute fonction homographique peut s'écrire sous la forme
f(x) = A +    B    
                x + d  
                      c
Démonstration:

f(x) =	ax + b
	cx +d

f(x) =	a(x + b/a)
	c(x + d/c)

f(x) =	a(x + d/c - d/c + b/a)
	c(x + d/c)

f(x) =	a(x + d/c) +  a(b/a -d/c)
	c(x + d/c)     c(x + d/c)

f(x) =	a +  a(b/a -d/c)
	c       c(x + d/c)

f(x) =	a  +  a   (b/a -d/c)
	c      c   (x + d/c)

On obtient bien la forme prévue avec:
A = a/c
B = a . (b/a – d/c)
       c

Ensemble de définition

Une fonction homographique est définie sur l'ensemble des nombres réels à l'exception du nombre pour lequel la fonction affine du dénominateur s'annule (puisque la division par zéro n'est pas possible). La valeur interdite de "x" est donc celle pour laquelle:
cx + d = 0
cx = -d
x = -d/c
Par conséquent l'ensemble de définition d'une fonction homographique est:
 ];-d/c[U]-d/c;[ que l'on peut aussi noter {-d/c}

Représentation graphique

La courbe qui représente une fonction homographique est une hyperbole (comme pour la fonction inverse). C'est une courbe qui possède un centre de symètrie de coordonnée (-d/c ; a/c) autour duquel les variations de la fonction
sont particulièrement importantes, il est donc nécessaire de réduire le pas entre les points du tableau de valeur pour obtenir une courbe fidèle.

Aspect général de la courbe d'une fonction homographique



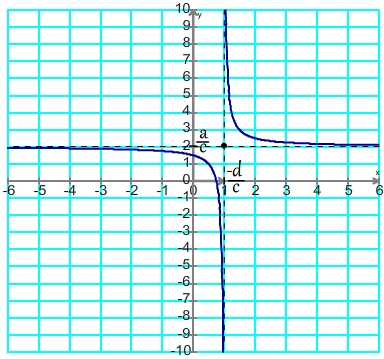
Antécédents

Chaque nombre de l'ensemble des réels possède, par une fonction homographique, un seul et unique antécédent à l'exception du nombre a/c qui n'en possède pas.
Trouver l'antécédent x1 d'un nombre y1 par une fonction homographique consiste à résoudre l'équation:

ax1 + b	=y1
cx1 +d

ax₁ + b = y₁(cx₁ +d)
ax₁ + b = y₁cx₁ +dy₁
ax₁ – y₁cx₁ = dy₁ – b
x₁(a-y₁c) = dy₁ – b

x1=	dy1 – b
	a – y1c

 

L'antécédent d'un nombre d'un nombre y1 par une fonction homographique est donc le nombre x1 =	dy1 – b
	a – y1c

mais ce nombre n'est pas défini lorsque le dénominateur ( a – y1c) s'annule ce qui confirme que le nombre a/c ne possède pas d'antécédent.

Variations

La forme réduite d'une fonction homographique permet de prévoir ses variations
f(x) = A +    B    
                x + d  
                      c
Si B est positif (ce qui revient à écrire que  b/a – d/c>0 ou encore que bc – da>0) alors la fonction homographiqe se comporte de manière comparable à la fonction inverse et elle est décroissante sur ];-d/c[ puis sur ]-d/c;[

  

Aspect de la courbe		Tableau de variations

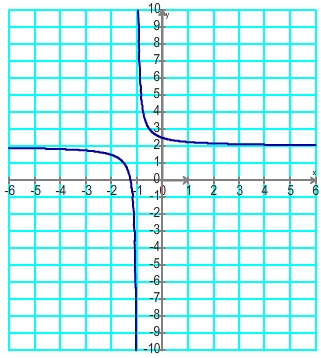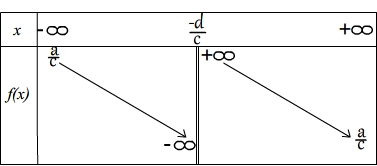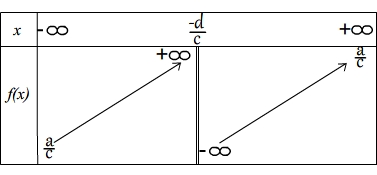
Si B est négatif ( ce qui revient à dire que  b/a – d/c<0 ou encore que bc – da<0) alors la fonction homographiqe est croissante sur ];-d/c[ puis sur ]-d/c;[

Aspect de la courbe		Tableau de variations

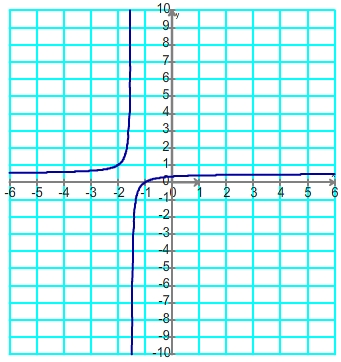Signe

Le signe de la fonction peut être déduit du signe des fonctions affines dont elle est le rapport, lorsquelles sont de même signe alors la fonction homographique est positive mais lorsqu'elles sont de signes différents alors la fonction homographique est négative.