Les fonctions - Classe de seconde

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Les fonctions - cours de seconde

Trigonométrie

Le cercle trigonométrique

Définition

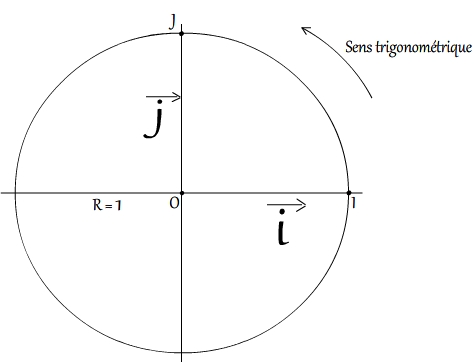
Le cercle trigonométrique est un cercle:
- dont le rayon est d'une unité
- dont le centre coïncide avec l'origine du repère orthonormé (O, , )
- dont le rayon horizontale droit coïncide avec le vecteur du repère orthonormé
- dont le rayon vertical supérieur coïncide avec le vecteur du repère orthonormé
- orienté dans un sens dit "trigonométrique" correspondant au sens  inverse des aiguilles d'une montre

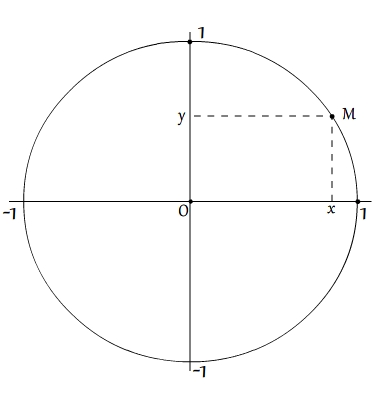
Repérage d'un point du cercle trigonométrique par ses coordonnées

Son abscisse, x, est la projection de M sur l'axe des abcsisses. Elle est comprise entre -1 et 1, elle prend des valeurs positives si M appartient à la moitiée droite du cercle et prends des valeurs négatives lorsqu'il appartient à la moitié gauche. Cette abscisse correspond au cosinus de l'angle associé à M.
 
Son ordonnées, y, est la projection de M sur l'axe des ordonnées. Elle est également comprise entre -1 et 1, elle prend des valeurs positives si M appartient à la moitié supérieure du cercle et prends des valeur négative lorsqu'il appartient à la moitiée inférieure. Cette ordonnée correspond au sinus de l'angle associé à M.

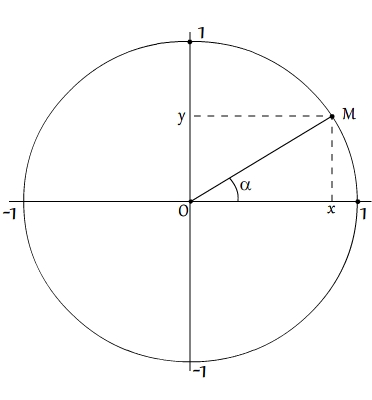
Repérage d'un point du cercle trigonométrique par un angle

Un point M du cercle peut aussi être repéré par l'angle α formé par (OM) et le vecteur unitaire . Inversement à chaque angle α il est possible d'associer un point M. Etant donnée que le cercle est orienté, l'angle est positif s'il exprimé suivant le sens trigonométrique et il est négatif dans le sens inverse.

Expression des angles

Dans le cercle trigonométrique, les angle sont de préférence exprimés en radian (symbole rad), il faut donct être capable de passer des degrés à cette unité (et inversement). La relation qui permet de faire la conversion est la suivante:

La conversion inverse (des radians aux degrés) se fait grâce à la relation suivante:

Les principales équivalences à retenir sont les suivantes:

Angle en degré	0	30	40	45	60	90	180
Angle en radian		π 6	2π 3	π 4	π 3	π 2	π

Remarque: toute angle est α est équivalent à l'angle α + 2π, ainsi qu'à α +4π, à α + 6π etc

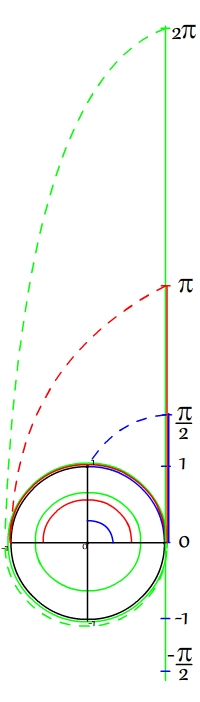
Enroulement de la droite des réels sur le cercle trigonométrique

"Enrouler la droite des réels sur le cercle trigonométrique" consiste à exprimer sur sur cette droite la longueur des arcs de cercle associés à chaque angle du cercle trigonométrique.
D'une manière générale, la longueur "d" d'un arc de cercle intercepté par un angle α dans un cerlce de rayon R peut être exprimée par la formule suivante:

                                                 d = α.R    
                                             
                                               où α est en radian
                                                    d et R sont exprimés avec la même unité de longueur

Remarque: la longueur de l'arc de cercle intercepté par un angle plein (2π) est, d'après cette formule, 2πR ce correspond bien à l'expression du périmètre d'un cercle.

Puisque, par définition, le cercle trigonométrique à un rayon égal à 1 alors l'expression des longueur des arcs de cercle devient:

                                                   d= α