Les fonctions - Classe de seconde
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Les fonctions - cours de seconde
Etude qualitative de fonctions
Les tableaux de variations
Qu'est-ce qu'un tableau de variation ?
Il résume les informations essentielles concernant les variations d'une fonction sur son ensemble de définition: il indique les intervalles sur lesquelles elle est croissante ou décroissante ainsi que l'image des nombres pour lesquels un extremum est atteint (valeur maximale ou minimale).
Un tableau de variation comporte toujours deux lignes:
- La première ligne indique les nombres clés de l'ensemble de définition, à savoir les bornes de ce derniers ainsi que les nombres qui délimitent les intervalles où la fonction est monotone (soit croissante, soit décroissante)
- La deuxième ligne du tableau indique, pour chaque intervalle de l'ensemble de définition, les variations de la fonction. Une flèche descendante signifie que la fonction est décroissante tandis qu'une flèche montante indique qu'elle est croissante. Par ailleurs chaque flèche est encadrée par l'image des nombres qui délimitent l'intervalle auquel elle est associée et chacune de ces images correspond à un extremum: Un maximum à l'origine et minimum à la pointe pour une flèche descendante et l'inverse pour une flèche montante.
Remarque: on ajoute parfois dans le tableau des valeurs ayant un intéret particulier comme par exemple les nombres de l'ensemble de définition pour lesquels la fonction est nulle (ce qui permet de repérer les intervalles pour lesquels la fonction prend des valeurs positives ou négatives)
Exemple de tableau de variations
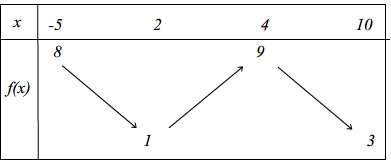
Ce tableau nous indique que:
- L'ensemble de définition de la fonction f est l'intervalle [-5 ; 10]
- f(-5) = 8
- f(2) = 1
- f(4) = 9
- f(10) = 3
- f est décroissante sur l'intervalle [-5 ; 2 ] et les images des nombres de cet intervalle sont comprises entre 1 et 8
- f est croissante sur l'intervalle [2 ; 4 ] et les images des nombres de cet intervalles sont comprises entre 1 et 9
- f est décroissante sur l'intervalle [4 ; 10] et les images des nombres de cet intervalle sont comprises entre 3 et 9
- Le maximum de f sur son ensemble de définition est 9
- Le minimum de f sur son ensemble de définition est 1
Réaliser un tableau de variations à partir d'une courbe
Il est possible d'utiliser la courbe représentative d'une fonction pour obtenir son tableau de variation en suivant la méthode suivante:
- Etape 1: distinguer les zones où la fonction est croissante ou décroissante.
- Etape 2: pour chacune des zones déterminer l'intervalle des abscisses qui lui est associé (trouver la borne inférieure et la borne supérieure) puis les reporter dans la première ligne du tableau de variations.
- Etape 3: Pour chaque intervalle de la première ligne du tableau de variations faire correspondre dans la deuxième une flèche montante lorsque la fonction est croissante et une flèche descendante lorsqu'elle est décroissante.
- Etape 4: Utiliser la courbe pour trouver l'image par f de chaque nombre figurant dans la première ligne (cette image correspond à l'ordonnée du point ayant ce nombre pour abscisse) puis, sous chaque nombre, reporter dans la deuxième ligne l'image trouvée (soit l'origine d'une flèche, soit à sa pointe).
Exemple: on souhaite réaliser un tableau de variations à partir de la courbe suivante
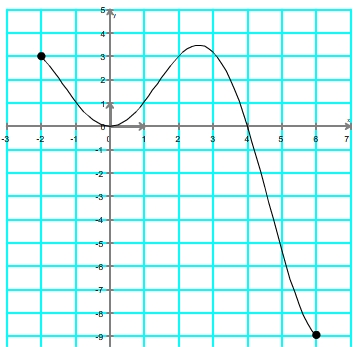
Etape 1
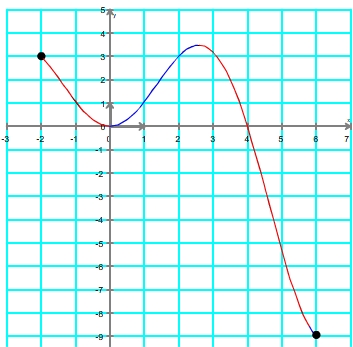
Etape 2
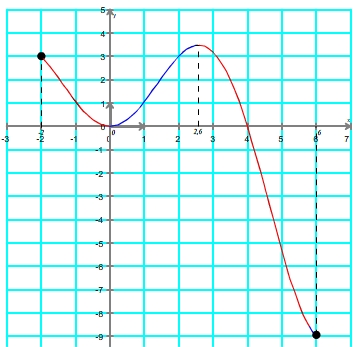

Etape 3
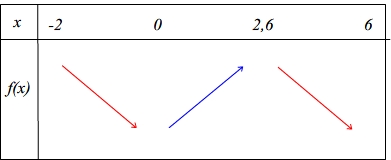
Etape 4
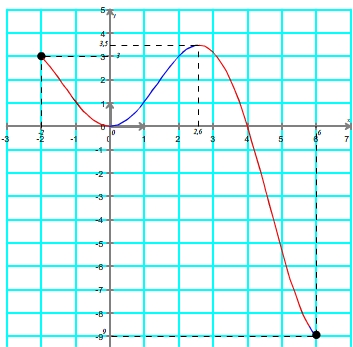
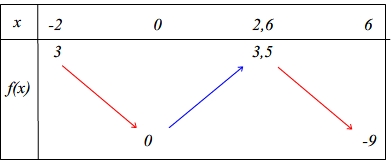
Tracer la courbe d'une fonction à partir de son tableau de variation
Etape 1: Utiliser le tableau de variation pour obtenir les coordonnées des points correspondant à chaque extremum (la première ligne indique les abscisses et la deuxième ligne fournit les ordonnées).
Etape 2: reporter ces point sur le graphique.
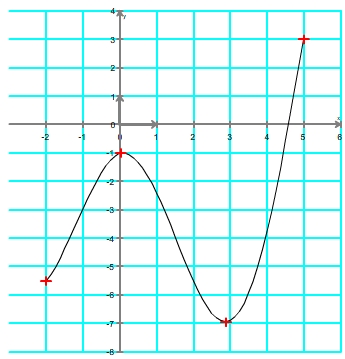
Etape 3: Tracer la courbe, sachant qu'entre deux points la fonction est monotone (soit toujours croissante, soit toujours décroissante).
Exemple de tracer d'une courbe à partir du tableau de variations suivant:
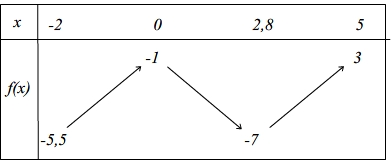
Etape 1
Les points à reporter sur le graphique ont pour coordonnées: (-2;-5,5), (0 ; -1), (2,8 ; -7) et (5 ; 3)
Etape 2
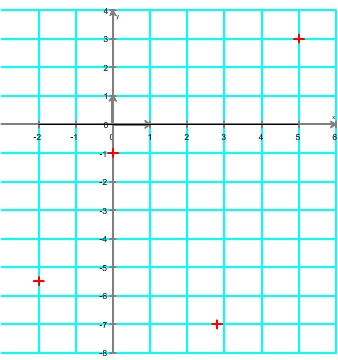
Etape 3
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
